Manuale Jasp

La verifica per carico limite dell'insieme fondazione-terreno è effettuato secondo l'approccio 2 (A1+M1+R3).

I coefficienti parziali di sicurezza, come riportato nei tabulati di stampa, utilizzati sono quelli indicati nel §6.4.3.1.1 NTC18 per le resistenze dei pali soggetti a carichi assiali, e quelli indicati nel §6.4.3.1.2 NTC18 per le resistenze dei pali soggetti a carichi trasversali.

Le resistenze assiali e trasversali sono calcolate con i metodi analitici di seguito indicati.

Carichi verticali

Il carico limite ultimo di un singolo palo per carichi verticali è ottenuto dall'equazione: ([3] §3.1.2 pag 74 e [8] §13.1.2 pag.372)

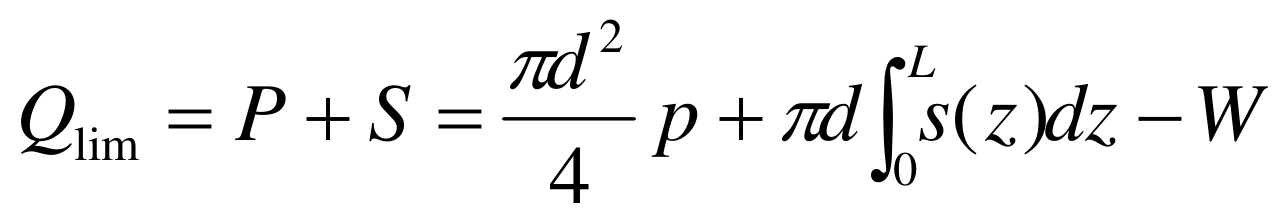
dove:

Qlim = carico limite ultimo assiale del palo singolo

P = Resistenza alla punta

S = Resistenza laterale

p = resistenza unitaria alla punta del palo singolo

s(z) = resistenza unitaria laterale alla generica profondità

W = peso proprio del palo

La resistenza unitaria alla punta (p) può  essere espressa mediante l'equazione :

p = Nq·σ'υ,z=L +Nc c

Che in condizioni non drenate si trasforma nell'equazione:

p = Rc (συ,z=L +Nc cu)

con:

Nc = 9;

Rc = 1 per argille non consistenti (indice di consistenza ≥0,5) ([2] §8.5.1.1 pag 377; [7] §3.1.2.1 pag.76)

Rc = (D +0,5)/(2D) ≤ 1per pali infissi in argille consistenti

Rc = (D +1)/(2D+1) ≤ 1per pali trivellati in argille consistenti

In condizioni drenate la resistenza unitaria alla punta (p) è calcolata con l'equazione:

p = Nq·σ'υ,z=L

Per il calcolo del coefficiente Nq si utilizzano le curve di Berezantev et al 1961 ( [8] §13.1 pag 377; [9] §2.4.2 pag.242)

dove:

φcal = (φ  + 40°)/2 per pali battuti

φcal = φ - 3°  per pali trivellati

Come abbiamo visto in precedenza la resistenza laterale S è pari a:

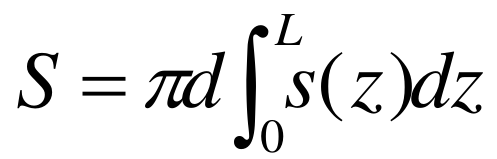
In condizioni drenate la resistenza laterale unitaria s(z) può  essere valutata mediante il cosiddetto "metodo β". Con questo metodo:

s(z) = μ K σ'υz

dove β = K·μ e μ=tg(δ)

Di seguito sono riportati i valori utilizzati da Jasp per terreni a grana grossa ( [8] §13.1 pag 378; [9] §2.4.2 pag.246)

Per densità  relative intermedie Jasp calcola il valore interpolato.

Per pali infissi in terreni a grana fine ( [10] §3.2.2.2 pag 24; [7] §3.1.2.1 pag.76)

K = K0 = (1-sinφ')·OCR0,5

per pali trivellati in argille consistenti (indice di consistenza ≥0,5)

K = (1 + K0)/2

In condizioni non drenate, quindi in caso di argille e limi saturi, la resistenza unitaria laterale è valutata con il cosiddetto "metodo α". In questo caso:

s(z) = α·cu

I valori di α possono essere calcolati come indicato di seguito: (protocollo Viggiani)

Pali trivellati: α = 0,7-0,008(cu - 25) , con 0,35 ≤ α ≤0,7

Pali battuti: α = 1-0,011(cu - 25) , con 0,5 ≤ α ≤1

oppure: (protocollo Lancellotta) ( [3] §3.1.2.1 pag 75;)

Pali trivellati (Stas e Kulhavy 1984) : α = 0,21 + 0,26·pa/cu

dove pa = pressione atmosferica

Pali infissi (Olson e Dennis 1982) :

Carichi orizzontali

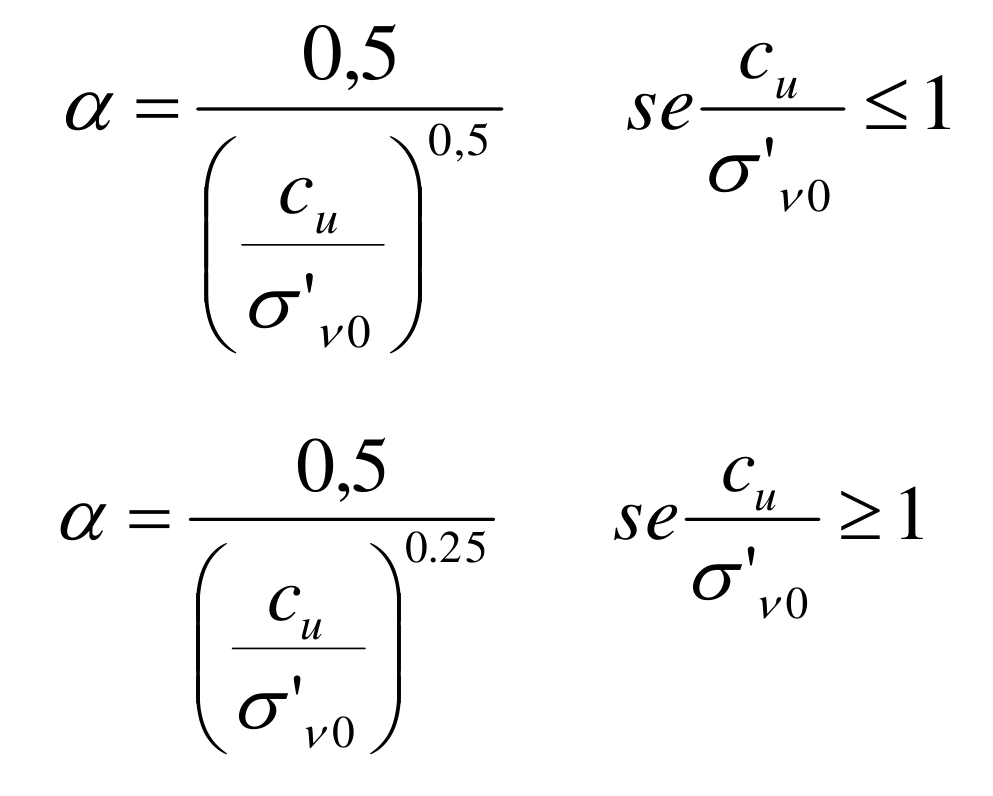
Il calcolo del carico limite orizzontale di pali orizzontali è riportato nel §13.2 di [8] e nel cap.7 di [10]. I risultati presentati nei riferimenti bibliografici sono calcolati ipotizzando un palo in un terreno omogeneo.

Jasp esegue un'analisi numerica per determinare il carico limite orizzontale di pali in terreni con diversi strati.

Per terreni coesivi la resistenza limite del terreno è posta pari a ( [10] fig.7.4 pag 152; [8] fig.13.22 pag.399)

pu = 9 c                 per profondità  ≥ 3D,

pu = cu [2+ 7z/(3d)]                         per z < 3D

per i terreni non coesivi ( [10] §7.2.2.2 pag 155; [9] fig.9.3.2.1 pag.265)

pu = 3σ'v Kp

dove:

σ'v = tensione litostatica verticale efficace

Kp = (1+sen φ')/(1-sen φ')

φ' = angolo di attrito interno (in tensioni efficaci)

Pali non vincolati o a testa libera

La rottura di un palo libero di ruotare in testa può  avvenire secondo due meccanismi:

a) a palo corto: senza la formazione di cerniere plastiche nel palo

b) a palo lungo, con la formazione di una cerniera plastica nel palo ad una profondità  da calcolare.

Jasp calcola, per ogni coppia Hu-Mu, il meccanismo di rottura e l'eventuale posizione della cerniera plastica, tenendo conto della resistenza limite dei diversi strati attraversati dal palo.

Pali vincolati o a testa incastrata

La rottura di un palo non libero di ruotare in testa può  avvenire secondo tre meccanismi:

a) a palo corto: senza la formazione di cerniere plastiche nel palo

b) a palo medio, con la formazione di una sola cerniera plastica in testa al palo.

c) a palo lungo, con la formazione una cerniera plastica in testa al palo e di un'altra cerniera ad una profondità  da calcolare.

Jasp calcola, per ogni forza orizzontale Hu, il meccanismo di rottura e l'eventuale posizione della cerniere plastiche, tenendo conto della resistenza limite dei diversi strati attraversati dal palo.

Gruppo di pali

Secondo EC7 §7.6.2.1 punti (3) e (4):

Per i pali in gruppo si devono prendere in considerazione due meccanismi di rottura:

- rottura per compressione dei singoli pali;

- rottura per compressione dei pali e del terreno compreso tra essi, considerati come un blocco unico.

Si deve assumere come resistenza di progetto il minore tra i valori dovuti a questi due meccanismi.

La resistenza a compressione del gruppo di pali, considerato come un blocco unico, si può  calcolare considerando il blocco come un palo singolo di grande diametro.

Per il calcolo della resistenza al carico verticale di un gruppo di pali Jasp calcola la resistenza del palo equivalente di grande diametro utilizzando i metodi di calcolo delle fondazioni diretta se L/D <5 e i metodi di calcolo delle fondazioni profonde se L/D >5

Jasp, oltre che alla procedura proposta dell'EC7, calcola il fattore E di efficienza della palificata come di seguito riportato ([8] §13.1.7 pag 396 e [10] §3.3.1.1 pag.32)

E = 1 per terreni incoerenti

Per un gruppo di m file con n pali ad interasse x in terreni incoerenti

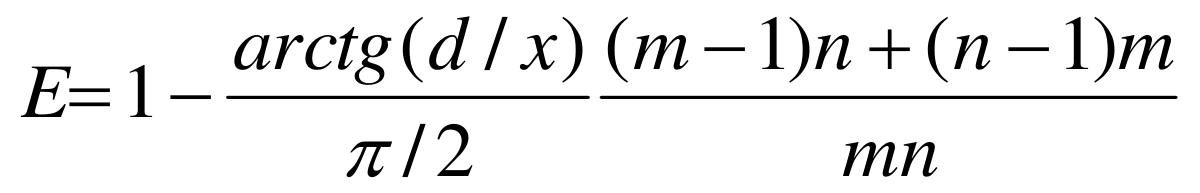
Nel caso in cui i pali attraversano strati coerenti e incoerenti Jasp calcola il fattore E come la media pesata dei valori sopra indicati, utilizzando come peso la portata degli strati.

Il coefficiente di gruppo in caso di carichi orizzontali è posto, forfettariamente a 0,5, se non indicato diversamente nel tabulato di stampa.([8] §13.2.6 pag 416 e [10] §7.3.1 pag.164)

Cedimenti

Per il calcolo dei cedimenti sotto i carichi di esercizio Jasp divide il palo in tanti conci elementari ed utilizza il metodo degli elementi finiti per il calcolo delle sollecitazioni e degli spossamenti del palo.

La costante di elasticità laterale verticale del terreno è calcolata con la formula:

kv = 2πG/ζ  [N/m²]       ([8] §14.1.2 pag 424)

dove: ζ= ln(2.5*(1-ν)*L/r0)       ([8] §14.1.2 pag 425)

La costante di elasticità della punta del palo è

kp = 2dE/(1- ν²) [N/m]       ([8] §14.1.2 pag 424)

La costante elastica orizzontale è calcolata con le formule ([8] §14.4.1 pagg 466, 487,479 e [10] §8.2.3 pag.180)

kh = 1.67·E/d per terreni a grana fine sovraconsolidati.

kh = nh·z/d , dove: nh = 0,5·106 [N/m³]per terreni a grana fine normalconsolidati. ([8] §14.4.1 pag 479)

kh = (Aγ'/1,35)·z/d       per terreni a grana grossa.

dove:

γ' è il peso dell'unità  di volume efficace.

A = 200 per terreni sciolti (Dr = 25%); A = 600 per terreni medi (Dr = 50%) ; A = 1500 per terreni sensi (Dr = 75%)

Nelle formule di questo paragrafo: G = modulo di elasticità  trasversale del terreno; ν = coefficiente di Poisson del terreno; L = lunghezza del palo; r0 = raggio del palo; d = diametro del palo; E = modulo di elasticità  longitudinale del terreno.

La verifica dei cedimenti differenziali è fatta come per le fondazioni dirette.

Tabelle di verifica

Jasp, per le verifiche geotecniche dei pali mostra le seguenti tabelle.

Coef. Verifiche Palo

In questa tabella sono riportati i risultati delle verifiche. In particolare sono riportati i seguenti coefficienti di verifica:

•Port. Dren: Coefficiente di verifica del palo per carichi verticali, per il terreno in condizioni drenate.

•Port. non Dren: Coefficiente di verifica del palo per carichi verticali, per il terreno in condizioni non drenate.

•Scorr. Dren: Coefficiente di verifica del palo per carichi orizzontali, per il terreno in condizioni drenate.

•Scorr. non Dren: Coefficiente di verifica del palo per carichi orizzontali, per il terreno in condizioni non drenate.

•Liquef.: Non applicabile par i pali.

•Tot SLU: Coefficiente totale di verifica della portata del palo.

•Ced. max:Coefficiente di verifica per dei cedimenti. La verifica dei cedimenti è fatta con la disuguaglianza: w ≤ 50mm , come indicato al §H(4) EC7-1:2005

•Ced. diff. Verifica dei cedimenti deferenziali come indicato nel paragrafo delle fondazioni dirette.

•Tot SLE: Coefficiente totale di verifica del palo agli stati limite di esercizio

•Totale : Coefficiente totale di verifica per gli SLU e gli SLE.

Carico Limite

In questa tabella sono riportati le resistenze medie, le resistenze caratteristiche e i coefficienti parziali di sicurezza per il calcolo delle resistenze di progetto, come riportato nel §6.4.3.1 delle NTC18

Per le verifiche geotecniche dei pali Jasp utilizza l'approccio 2.

Coefficienti parziali γR (Tabella 6.4.II NTC18):

•γb: Coefficiente parziale per la resistenza di base.

•γs: Coefficiente parziale per la resistenza laterale in compressione.

•γst : Coefficiente parziale per la resistenza laterale in trazione.

•γT : Coefficiente parziale per i carichi trasversali.

Inoltre, a partire dalla stratigrafia media e a partire dalla stratigrafia peggiore Jasp calcola i seguenti valori.

•E Gruppo: Fattore di efficienza del gruppo.

•ξ: Fattore di correlazione funzione del numero di verticale indagate come riportato nella tabella 6.4IV NTC18.

•Rcks Dr. [N]: Resistenza caratteristica laterale del palo in condizioni drenate.

•Rckb Dr. [N]: Resistenza caratteristica di base del palo in condizioni drenate.

•Rcks N.Dr. [N]: Resistenza caratteristica laterale del palo in condizioni non drenate.

•Rckb N.Dr. [N]: Resistenza caratteristica di base del palo in condizioni non drenate.

Per la resistenza ai carichi orizzontali il programma riporta:

•E Gruppo:Fattore di efficienza del gruppo di pali orizzontali. Assunto pari a 0.5 in caso di pali al disotto del plinto e 1 in caso di pali isolati.

•Rot. testa: Il palo è considerato libero se è un palo isolato e non vi sono travi o piastre che si collegano ad esso.

Portate di progetto

In questa tabella sono riportate le portate di progetto in condizione drenata e non drenata.

Verifiche per combinazione

In questa tabella sono riportati i risultati delle verifiche agli SLU per ogni combinazione di carico.

Nel caso di forza orizzontale e palo con testa non vincolata le verifiche devono essere fatte confrontando la coppia m-fh che agisce sulla e la coppia hU-mU resistente.

Strati

Nella tabella strati sono riportati, per ogni strato, i parametri per il calcolo della portata orizzontale e verticale del palo. Per il calcolo della portata il palo è suddiviso in tanti conci.

•xIni e xFin: La quota iniziale e finale del concio ,a partire dalla testa del palo .

•zIni e zFin: La profondità dello strato di terreno.

•α: Parametro α per l'applicazione del metodo alfa, per condizioni non drenate.

•cu: Coesione non drenata

•β: parametro β per l'applicazione del metodo beta

•k: parametro k per l'applicazione del metodo beta

•δ: parametro δ per l'applicazione del metodo beta, dove β = k·tg(δ)

•fs [Pa]: resistenza laterale per unità di superficie

•qs [N]: portata del tratto di palo

•fx Lim [N/m]: portata per carichi orizzontali del tratto alla profondità indicata.

Portata assiale

 

In questa tabella sono riportati i dati riassuntivi della del calcolo della portata assiale del palo. In particolare

•Q [N] : Portata verticale totale del palo. Q = Qs+Qb

•Qs [N]: Portata verticale laterale del palo.

•Qb [N]: Portata di base del palo.

•Nq: Coefficiente Nq calcolato utilizzando le curve di Berezantev.

•fi: φcal per le curve di Berezantev.

•cuBase: coesione non drenata dello strato al disotto della punta del palo.

•Gran Inf.: Tipo di terreno dello strato ad disotto della punta del palo.

•σVo: Pressione litostatica totale alla punta del palo

•σ'vo: Pressione litostatica efficace alla punta del palo

Strato punta

In questa tabella è riportato lo strato posto immediatamente al disotto della punta del palo.

Portata laterale palo a testa vincolata

In questa tabella sono riportati i risultati più significativi del calcolo della portata laterale del palo a testa vincolata. In particolare è riportato:

•Tipo: Tipo di comportamento (corto/medio/lungo)

•Hu [N]: Portata laterale

•Mmax [Nm]: Momento massimo nel palo ipotizzando il comportamento a palo corto.

•x Medio [m]: Ipotizzando il comportamento a palo medio, posizione del punto che non subisce spostamenti orizzontali.

•Cer1 [m]: Posizione della prima cerniera plastica.

•My1 [Nm]: Momento resistente della prima cerniera plastica

•Cer2 [m]: Posizione della seconda cerniera plastica.

•My3 [Nm]: Momento resistente della seconda cerniera plastica

•ξ: Fattore di correlazione ξ ricavato dalla tabella 6.4.IV NTC18

Portata laterale palo a testa libera

In questa tabella sono riportati i risultati più significativi del calcolo della portata laterale del palo a testa libera. Per un palo a testa libera, come si vede dal grafico seguente, il comportamento può dipendere dalla coppia di valori Hu-Mu. Nella tabella è riportata la portata laterale per Hu=0, per Mu=0 e dell'eventuale punto in cui si ha il passaggio da comportamento da palo corto a palo lungo. Nella colonna x è riportata la posizione, a partire dall'alto, dell'eventuale cerniera plastica.

Conci FEM Sezione palo

Per il calcolo delle sollecitazioni e degli spostamenti del palo Jasp utilizza un modello a elementi finiti ad hoc. In questa tabella sono riportati i dettagli del modello ed in particolare dei vincoli utilizzati. In particolare, tra l'altro, è riportato:

•kh [N/m³]: La costante elastica orizzontale del terreno.

•kb [N/m]: La costante di elasticità verticale del terreno della punta del palo.

•kv [N/m²]: La costante di elasticità laterale verticale del terreno.

•ko_inf [N/m]: Rigidezza agli spostamenti orizzontali del vincolo posto nella parte inferiore del concio. ko_inf = Δz·kh·d;

•kz_inf [N/m]: Rigidezza agli spostamenti verticali del vincolo posto nella parte inferiore del concio. kz_inf = Δz·kv + kb

•kt inf [Nm]: Rigidezza alle rotazioni lungo l'asse z del vincolo posto nella parte inferiore del concio. kr_inf = kv·Δz·r².

•kr inf [Nm]: Rigidezza alle rotazioni lungo l'asse x [y] del vincolo posto nella parte inferiore del concio. kr_inf = kv·Δz³.

dove d è il diametro del palo, r il raggio e Δz la lunghezza del concio.

Matrice Totale vincolo sup.

Per calcolare la struttura in elevazione Jasp modella l'intero palo con un vincolo cedevole posto alla sommità del palo, eliminando così, ai fini del calcolo della parte in elevazione, l'intera modellazione FEM del palo. In questa tabella è riportata la matrice di rigidezza del vincolo cedevole utilizzato per modellare l'intero palo.

---

[1] R. Lancellotta; Goetecnica, IV Edizione, Zanichelli 2012.

[2] M.Tanzini;Fondazioni, Dario Flaccovio Editore 2006

[3] Lancellotta Costanzo Foti; Progettazione Geotecnica, Hoepli 2011

[4] AA.VV. Guida all'Eurocodice 7, Thomas Telford 2005, EPC Editore 2012

[5] AA.VV. Guida all'Eurocodice 8, Thomas Telford 2005, EPC Editore 2012

[6] G. Riga;La liquefazione dei terreni, Dario Flaccovio Editore 2007

[7] Lai, Foti, Rota; Input sismico e Stabilità Geotecnica dei Siti in Costruzione, IUSS Press 2009

[8] A.Castellani, E.Faccioli;Costruzioni in zona sismica, Hoepli 2008

[9] Diego Carlo Lo Presti, Manuale di Ingegneria Geotecnica Vol I e II , Pisa University Press 2015

[10] H.G.Poulos E.H Davis, Pali, Dario Flaccovio Editore 1987