Fondazioni dirette
Le verifiche geotecniche eseguite da Jasp sono:
• Portanza drenata.
• Portanza non drenata (terreno a grana fine saturo).
• Scorrimento drenato.
• Scorrimento non drenato (terreno a grana fine saturo).
• Liquefazione terreno (sisma con sabbie sature).
• Cedimenti edometrici (per terreno a grana fine).
• Cedimenti con metodo di Burland e Burbidge (per sabbie).
• Cedimenti differenziali.
Esse riguardano i seguenti tipi di fondazioni:
• Plinto diretto: Fondazione superficiale costituita da un blocco in calcestruzzo armato a forma di parallelepipedo su cui è presente un solo pilastro e/o un solo carico concentrato.
• Trave rovescia: Trave di fondazione con una dimensione prevalente che per le verifiche geotecniche è considerata di lunghezza infinita.
• Platea: Fondazione superficiale con 2 dimensioni prevalenti su cui di norma sono presenti più pilastri e/o carichi distribuiti. In generale le platee di fondazione hanno forma qualsiasi, prevalentemente poligonale o circolare, ma per le verifiche geotecniche di seguito riportate esse sono approssimate con un rettangolo di area equivalente. La posizione e il rapporto B/H del rettangolo equivalente sono uguali a quelli dell'ellisse centrale di inerzia della impronta originale.
Per ogni rettangolo di fondazione Jasp riporta i seguenti dati:

In questa tabella le coordinate del punto centrale della fondazione sono espresse nel sistema di riferimento globale.
La verifica per carico limite dell'insieme fondazione-terreno è effettuata secondo l'approccio 2 (A1+M1+R3) con i seguenti coefficienti parziali di sicurezza:
γG1 = 1,3; γG2 = 1,5; γQi = 1,5; γR = 2,3; γM = 1,0;
La verifica della capacità portante viene fatta come indicato nell'appendice D dell' EC7-1-2005 secondo il procedimento di seguito riportato.
In ogni caso, sia per le verifiche geotecniche delle travi rovesce che delle platee di fondazione, Jasp mostra nelle seguenti tabelle i carichi in fondazione utilizzati per le verifiche ed i parametri geotecnici di partenza.




Tutti i dati sono relativi al sistema di riferimento della fondazione, con l'origine al centro del rettangolo di fondazione , l'asse x parallelo al lato maggiore del rettangolo di fondazione.
Simboli utilizzati
q= pressione litostatica totale di progetto agente sul piano di posa della fondazione;
q'= pressione litostatica efficace di progetto agente sul piano di posa della fondazione;
B'= larghezza efficace di progetto della fondazione;
L' =lunghezza efficace di progetto della fondazione;
A' = B'·L' = area della fondazione efficace di progetto (per le travi: A' = B'·1m);
B'/L' ≤ 1 (per le travi: B'/L' = 0);
D= profondità del piano di posa;
γ'= peso di volume efficace di progetto del terreno al di sotto del piano di posa della fondazione;
V = carico verticale;
H = carico orizzontale;
θ = angolo che H forma con la direzione L';
R = Resistenza totale fondazione;
cu = Resistenza a taglio non drenata;
c': = Coesione intercetta in termini di tensioni efficaci;
φ' = Angolo di resistenza a taglio in termini di tensioni efficaci;
φ'cv = angolo di resistenza a taglio allo stato critico;
Il carico limite di progetto si calcola con la formula:
R/A' = σc·cu·dc·sc·ic + σq
dove:
σc = (2 + π)
σq = q
sc = 1 + 0,2 (B'/L')
ic = ½+ ½[1 - H/(A'·cu)]0,5 con H ≤ A'·cu
dc = 1 + 0,4 atg(D/B')
dove il coefficiente di profondità dc è calcolato come indicato da Meyerof (1951), Skempton (1951) e Hansen 1961 ( [1] §8.17.2 pag 437; [2] §4.2 pag 117 )
Nel caso di suoli con più strati, la resistenza portante è calcolata utilizzando i parametri dello strato meno resistente. La ricerca dello strato meno resistente viene fatta tenendo presente il meccanismo di collasso non drenato interessa un zona con profondità 0,707·B ( [1] §8.13.1 pag 412, fig.8.51 ).
Jasp crea la seguente tabella riassuntiva per le verifiche del carico limite per le condizioni non drenate:

Il carico limite di progetto è calcolato con la formula:
R/A' = σc·Nc·dc·sc·ic + σq·Nq·dq·sq·iq + σγ·Nγ·dγ·sγ·iγ
con:
σc = c'
σq = q'
σγ = 0,5 γ' B'
e con i valori di progetto dei fattori adimensionali per
- la resistenza portante:
Nq = eπtanφ' tan²(45° φ'/2)
Nc = (Nq -1) ctg φ'
Nγ = 2(Nq -1) tg φ'
- la forma della fondazione:
sq = 1 + (B'/L') sen φ'
sc = (sq·Nq -1)/( Nq -1)
sγ = 1- 0,3(B'/L')
- la profondità della fondazione (Hansen 1970, Vesic 1973) ( [1] §8.17.1 pag 435; [2] §4.2 pag 117 )
dq = 1+ 2 tg φ' (1 – sin φ')² atg(D/B')
dc = dq – (1-dq)/(Nc·tgφ')
dγ = 1
- l'inclinazione del carico, dovuta ad un carico orizzontale H che forma un angolo θ con la direzione di L',
iq = [1 - H/(V + A'c'cotφ')]m;
ic = iq - (1 - iq)/(Nc·tanφ');
iγ = [1 - H/(V + A'·c'·cotφ')]m+1;
dove:
m = mL cos²θ + mB sin²θ
mB = [2 + (B '/L')] / [1 + (B '/L')]
mL = [2·B '/L' + 1] / [1 + (B '/L')]
Nel caso di suoli con più strati, la resistenza portante è calcolata utilizzando i parametri dello strato meno resistente. La ricerca dello strato meno resistente viene fatta tenendo presente che il meccanismo di collasso drenato interessa una zona con profondità z = B sinψ exp(ψ tgφ') con ψ = 45° + φ'/2 ( [1] §8.13.1 pag 430, fig.8.59 ).
Jasp crea la seguente tabella riassuntiva per le verifiche del carico limite per le condizioni drenate:

Verifica sismica SLV
Gli effetti sismici sono tenuti in conto come indicato nei §7.11.5.3 NTC18 e §C7.11.5.3.1 CNTC18.
In particolare l'effetto inerziale e portato in conto nel calcolo delle forze orizzontali H trasmesse dalla fondazione al terreno ed impiegando le formule comunemente adottate per calcolare i coefficienti correttivi del carico limite in funzione dell'inclinazione, rispetto alla verticale, del carico agente sul piano di posa.
L'effetto cinematico, che modifica il solo coefficiente Nγ, è tenuto in conto con l'introduzione di una forza orizzontale aggiuntiva Hk = kvk·V, con kvk calcolato come indicato nel §7.11.3.5.2 NTC18
La verifica per scorrimento sul piano di posa è effettuato secondo l'approccio 2 (A1+M1+R3) con i seguenti coefficienti parziali di sicurezza:
γG1 = 1,0; γG2 = 1,0; γQi = 1,0; γR = 1,1; γM = 1,0
Il calcolo della resistenza allo scorrimento è fatto come indicato nel §6.5.3 EC7-1:2005 ( [4] §3.3.2 pag 96; [3] §2.5 pag 41)
La verifica a scorrimento in condizione drenate è fatta con la relazione:
H ≤ Rd
Dove:
•in condizioni drenate: Rd = V·tg φ'cv/γR
•in condizioni non drenate: Rd = A·cu/γR
con A = area della fondazione.
Jasp crea la seguente tabella riassuntiva per le verifiche a scorrimento:

La verifica della liquefazione è svolta come indicato nel §7.11.3.4.2 NTC08.
Il calcolo della magnitudo attesa è effettuato utilizzando, a partire dal reticolo di riferimento fornito nell'allegato B delle NTC08, la formula di Sabetta e Pugliese (1996) ([8] §1.5 pag.9)
log(A) = -1,562 + 0,306 M – Log[(de² + 5,8²)1/2] (1)
dove:
A è l'accelerazione massima attesa in g
de è la distanza dall'epicentro del sisma in km.
Per il calcolo della magnitudo attesa per il sito in oggetto si è proceduto in questo modo:
a) Tutti i 10751 punti del reticolo sono ipotizzati (a vantaggio di sicurezza) come possibili epicentri di sisma e utilizzando la formula inversa della (1) sono calcolate tutte le magnitudo di tutti i possibili terremoti in Italia.
b) Riutilizzando la (1) a partire da ogni punto del reticolo vene calcolata l'accelerazione nel sito in oggetto, scartando i terremoti che producono un accelerazione attesa minore di 0,1g.
c) Tra tutti i terremoti non scartati si prende quello con magnitudo massima.
In questo modo, per il sito in esame si trova il sisma che ha magnitudo massima e che produce un'accelerazione maggiore di 0,1g , ovvero che può produrre la liquefazione del terreno.
La verifica a liquefazione può essere omessa quando si manifesta almeno una delle seguenti circostanze:
1) accelerazioni massime attese al piano campagna in assenza di manufatti (condizioni di campo libero) minori di 0,1g;
2) profondità media stagionale della falda superiore a 15 m dal piano campagna, per piano campagna sub-orizzontale e strutture con fondazioni superficiali;
Nel caso di sabbie in cui sia obbligatorio effettuare la verifica a liquefazione, per ogni strato di terreno posto al di sotto del piano di posa e potenzialmente liquefacibile, si procede con la verifica: ([2] §11.5.4 pag 401; [5] §10.4.1.5 pag 295; [6]; [7] §6.2.4 pag 243; [8] §9.3 pag.276) :
CSR*1,25/CRR ≤ 1
dove:
CSR = rapporto di sforzo ciclico;
CRR = rapporto di resistenza ciclica;
1,25 è il coefficiente di sicurezza definito dall'EC8-5 §4.1.4 (11) ;
con:
CSR = 0,65·rd·(amax/g)·(σf/σ'f) ;
amax = accelerazione orizzontale di picco SLV del sito in oggetto = S·ag = Ss·St·ag (NTC08§3.2.3.2) ;
σf = ΔσV+ σV0 = pressione verticale totale;
σ'f = ΔσV+ σ'V0 = pressione efficace verticale totale;
ΔσV è l'incremento di tensione prodotto dal carico netto, calcolato trascurando la rigidezza della fondazione e modellando il suolo con un semispazio elastico.
σ'V0 è la tensione geostatica efficace
σV0 è la tensione geostatica totale
g è l'accelerazione di gravità;
rd = 1 – 0,00765 z, per z ≤ 9.15 m;
rd = 1,174 – 0,00267 z, per 9.15 m < z ≤ 23 m;
z è la profondità in metri dal piano di campagna;
CRR = CRR7,5·CM;
dove: CRR7,5 = (a+c·x+e·x²+g·x³ )/(1+b·x+d·x²+f·x³+h·x4) ;
con: a=0.048; b=-0.1248; c=-0.004721; d=0.009578; e =0.0006136; f=-0.0003285; g=-0.00001673; h =0.000003741 (Blake 1996) ;
x = (N1)60CS = α + β N60 CN CP;
CN = (pa/σ'v0)1/2 con 0,5 ≤ CN ≤ 2;
pa = pressione atmosferica del sito in oggetto
CP = 0,75 per z ≤ 3m e CP = 1 per z > 3m;
N60 = NSPT normalizzato tenendo conto del rapporto energetico del maglio, diametro del foro, lunghezza delle aste e metodo di campionamento (vedere relazione geologica)
α e β dipendono dal contenuto di fino FC, con:
• FC ≤ 5%: α = 0,0 ; β= 1,0;
• 5% < FC ≤ 35%: α = exp[1,76 – (190/FC²)]; β= 0,99 + FC1,5/1000;
• 35% < FC: α = 5,0 ; β= 1,2;
CM dipende dalla magnitudo attesa M ed è ricavabile dalla Tabella B.1 EC8-5:2005 [Ambraseys (1988)], che approssimeremo per semplicità, ed a vantaggio di sicurezza, con le seguenti funzioni:
CM = (M/7,5) -3.3 per M≤7,5 [Andrus e Stokoe. (1997)]
CM = (M/7,5) -6.47 per M>7,5
La verifica globale per il rischio di liquefazione viene eseguita attraverso l' indice del potenziale di liquefazione LPI ([7] §6.2.4.3 pag 259 ) [Iwasaki et al. 1978] , che è definito dalla segnate formula
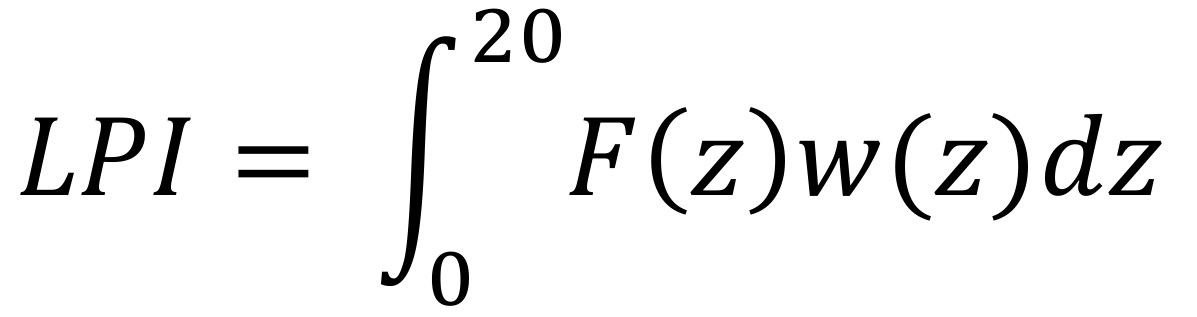
dove z è la profondità del piano di campagna espressa in metri, F e una funzione del fattore di sicurezza nei confronti della liquefazione FSL = CRR/CSR alla profondità z data da:
F(z) = 1-FSL(z) per FSL(z)≥1
F(z) = 0 per FSL(z)<1
e w(z) è una funzione della distanza dall'elemento di volume al piano di campagna, data da:
w(z) = 10 - 0,5z
La correlazione tra l'indice PLI e il potenziale di rottura è riportato nella seguente tabella:
Il coefficiente di verifica è pari a LPI/5, cioè se LPI>5 la verifica a liquefazione non è superata.
Jasp crea le seguenti tabelle riassuntive per le verifiche a liquefazione:


Con il coefficiente di verifica pari a -1 si intende “verifica non effettuata".
La verifica dei cedimenti è fatta con la disuguaglianza:
w ≤ 50mm
come indicato al §H(4) EC7-1:2005
Il calcolo dei cedimenti è effettuato con:
• il metodo edometrico per i terreni a grana fine (limi ed argille)
• il metodo Burland e Burbidge per i terreni a grana grossa (sabbie e ghiaie)
Per terreni a grana fine i cedimenti sono calcolati utilizzando il metodo edometrico, proposto da Terzaghi (1943) ( [1] §8.7.2 pag 437; [2] §5.3.2 pag.164; [3] §2.7 pag.58)
Il terreno al di sotto della fondazioni viene diviso in n strati e per ogni strado si calcola il cedimento con la formula
ΔHi = Hi [ RR·Log(kR) + CR·Log(kC) ]
con:
kR = min{σ'P ; σ'f }/σ'V0
kC = max{σ'f /σ'P ; 1}
σ'V0 è la tensione geostatica efficace
ΔσV è l'incremento di tensione prodotto dal carico netto, calcolato trascurando la rigidezza della fondazione e modellando il suolo con un semispazio elastico.
σ'f = ΔσV+ σ'V0
σ'P = tensione di preconsolidazione = OCR · σ'V0
dove OCR è il rapporto di preconsolidazione.
Hi = spessore dello strato
RR = rapporto di ricompressione
CR = rapporto di compressione
Per terreni normalconsolidati CR = 2,3·σ'V0/Eed
Per terreni sovraconsolidati RR = 2,3·σ'V0/Eed
dove Eed è il modulo edometrico.
Il cedimento totale è calcolato sommando il sedimento di tutti gli strati in cui ΔσV > 0,10 σ'V0
w = Σ ΔHi
Per argille tenere il metodo fornisce il cedimento di consolidazione ed il cedimento immediato è pari al 10% del cedimento di consolidazione
Per fondazioni su argille consistenti il metodo fornisce il cedimento totale.
Jasp crea le seguenti tabelle riassuntive per le verifiche dei cedimenti con il metodo edometrico:


Il calcolo dei cedimenti per i terreni a grana grossa è effettuato con il metodo di Burland e Burbidge (1985) ( [1] §8.8.1 pag 482; [2] §5.2.1 pag.153; [3] §2.8.1 pag.62 )
Il cedimento totale è calcolato con la formula :
w = fs·fh·ft·ZI·Ic·(σA/3 + σB)
dove:
σA = min{σ'P; q}
σB = max{q' - σA ; 0}
σ'P = tensione di preconsolidazione al piano di posa della fondazione = OCR · σ'V0
ZI = B 0,7 = profondità di influenza
B è la larghezza minima della fondazione espressa in m
L è la lunghezza della fondazione (L>B)
q' è il carico unitario efficace della fondazione espresso in kPa
Ic = 1,7/Nc1,4 = indice di compressibilità
Nc è la media aritmetica dei valori Ncs per la profondità H
con:
H = spessore dello strato comprimibile, se H < ZI
H = ZI, se NSPT è costante o cresce con la profondità
H = 2B, se NSPT decresce con la profondità
e, per ogni strato:
Ncs = 15 + (NSPT-15)/2 per sabbie fini o limose sotto falda con NSPT>15
Ncs = NSPT negli altri casi.
inoltre:
fh = kHZ/(2 - kHZ)
kHZ= min{1, H/ZI}
fs = [1,25 / (1+ 0,25·B/L )]²
ft = (1,3 + 0,2·Log(t/3)) con t la vita nominale della struttura in anni.
Jasp crea la seguente tabella riassuntiva per le verifiche dei cedimenti con il metodo di Burland e Burbidge:

La verifica dei cedimenti differenziali è fatta con la disuguaglianza:
Δw/ L ≤ 1/500
come indicato al §H(2) EC7-1:2005
dove:
L è la distanza tra i due punti di calcolo dei cedimenti considerati
Δw = |w1 – w2| = differenza tra i cedimenti considerati
In caso di trave di fondazione il calcolo è effettuato tra i cedimenti calcolati nelle sezioni iniziale, centrale e finale della trave.
Nel caso di plinti il calcolo viene effettuato tra ogni coppia di plinti.
Nel caso di platea il cedimento differenziale è calcolato tra il punto centrale e lo spigolo della platea considerando la platea di rigidezza nulla e posta su un semispazio elastico. In questo caso: Δw = w/2.
[1] R. Lancellotta; Goetecnica, IV Edizione, Zanichelli 2012.
[2] M.Tanzini;Fondazioni, Dario Flaccovio Editore 2006
[3] Lancellotta Costanzo Foti; Progettazione Geotecnica, Hoepli 2011
[4] AA.VV. Guida all'Eurocodice 7, Thomas Telford 2005, EPC Editore 2012
[5] AA.VV. Guida all'Eurocodice 8, Thomas Telford 2005, EPC Editore 2012
[6] G. Riga;La liquefazione dei terreni, Dario Flaccovio Editore 2007
[7] Lai, Foti, Rota; Input sismico e Stabilità Geotecnica dei Siti in Costruzione, IUSS Press 2009
[8] A.Castellani, E.Faccioli;Costruzioni in zona sismica, Hoepli 2008
